João Pedro - 7ºB, construiu a PIRÂMIDE DE SIERPINSKI, após as vídeo-aulas de Simetria. 
Um artista!!
O Triângulo de Sierpinski - também chamado de Junta de Sierpinski - é uma figura geométrica obtida através de um processo recursivo. Ele é uma das formas elementares da geometria fractal
por apresentar algumas propriedades, tais como: ter tantos pontos como o
do conjunto dos números reais; ter área igual a zero; ser
auto-semelhante (uma sua parte é idêntica ao todo); não perder a sua
definição inicial à medida que é ampliado. Foi primeiramente descrito em
1915 por Waclaw Sierpinski (1882 - 1969), matemático polonês.
Trata-se de um conjunto autossimilar de um triângulo (na maioria das
vezes equilátero). Se dividido em quatro outros triângulos congruentes
entre si e entre o triângulo original, cujos vértices são os pontos
médios do triângulo de origem, então os subconjuntos do fractal são três
cópias escalonadas de triângulos derivados da iterada anterior. O
triângulo do meio não pertence ao fractal. Esta separação do fractal em
cópias escalonadas pode ser continuada recursivamente nos outros
triângulos produzidos.
Construção
Uma das maneiras de se obter um triângulo de Sierpinski é através do seguinte algoritmo:
- Comece com qualquer triângulo em um plano. O triângulo de Sierpinski canônico utilizava um triângulo equilátero com a base paralela ao eixo horizontal, mas qualquer triângulo pode ser usado (ver primeira figura).
- Encolha o triângulo pela metade (cada lado deve ter metade do tamanho original), faça três copias, e posicione cada triângulo de maneira que encoste nos outros dois em um canto (ver segunda figura).
- Repita o passo 2 para cada figura obtida, indefinidamente (ver a partir da terceira figura).
Embora no processo acima a figura inicial seja um triângulo, não é necessário partir de um para se chegar no triângulo de Sierpinski. É possível utilizar qualquer figura geométrica (ver abaixo), o triângulo só é utilizado por facilitar a visualização.
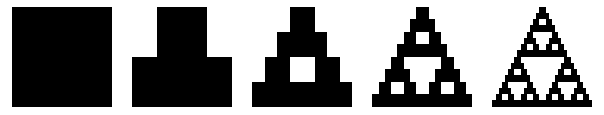
Março 2015
Nenhum comentário:
Postar um comentário